
VAE(変分オートエンコーダ) 解説
記事の目的
この記事では、VAEの仕組みについて解説します。VAEの構造や損失関数については解説しますが、パラメータの学習(勾配法、誤差逆伝播法)については解説を省略しています。上記の知識については、下の記事を参考にしてください。
目次
1. 使用するデータ
使用するデータはdigitデータで、8×8=64次元のデータです。以下の画像のように、0-9の数字画像のデータです。このデータを使用してVAEの構成を解説していきます。
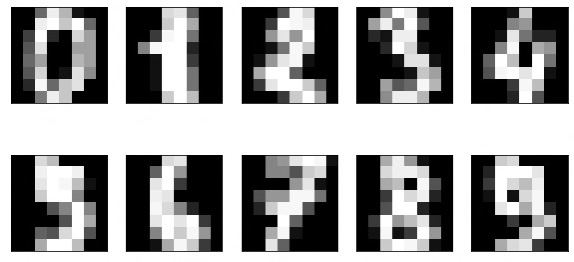
2. VAEの概要
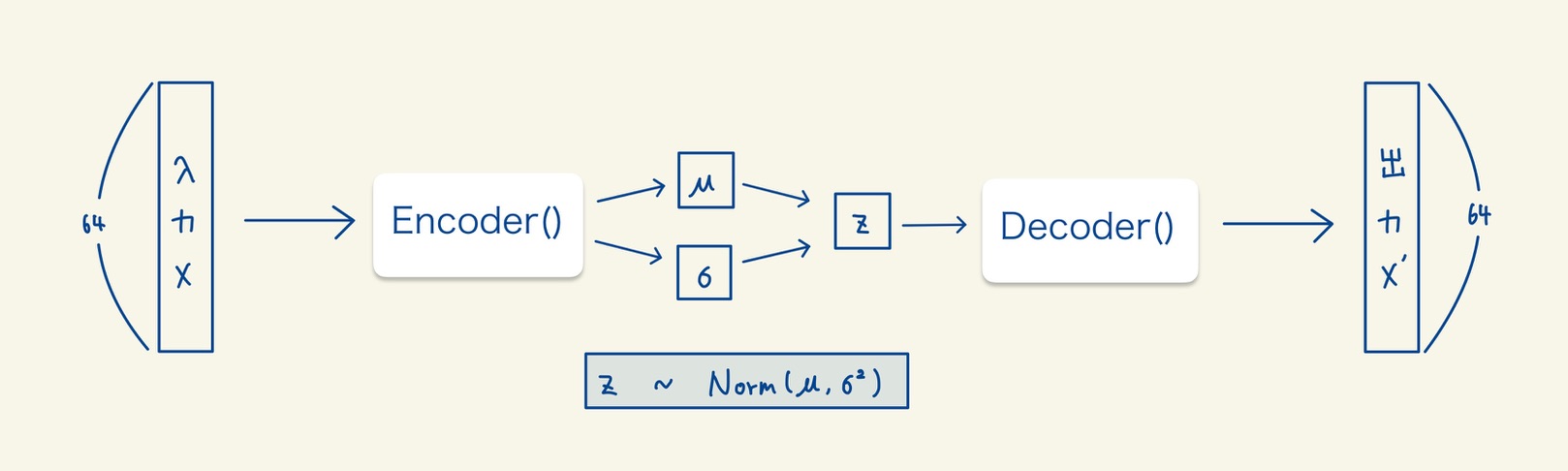
2.1 VAEの全体図
VAEの全体像は以下の図のようになっています。まず、画像データを入力としてEncoder()を通してμとσを出力します。そして、μを平均、σを標準偏差とした正規分布から乱数zを発生させます。zは潜在変数と呼ばれ、確率変数となります。さらに、このzからDecoder()を通して入力のデータに近いデータを出力します。
2.2 VAEのできること
潜在変数zを連続的に値を変化させることで、連続的な画像データを生成することができます。以下の写真が、実際に生成した連続的な画像データです。zは二次元のベクトルで、各次元の値を-3から3まで連続的にずらして生成した画像となっています。

3. VAEの構造
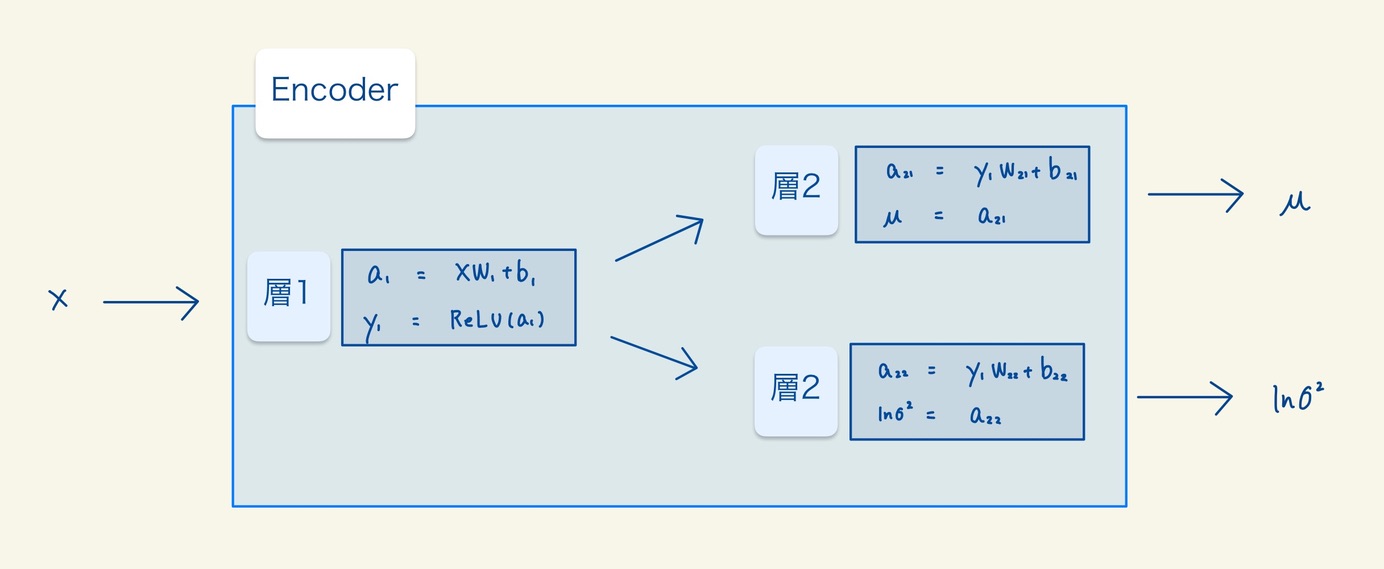
3.1 Encoderの構造
Encoderの構造は以下の図のようになっています。層は合計で3つありますが、μとσを出力するそうは構造が全く同じなのでどちらとも層2としました。EncoderのパラメータはW1, b1, W21, b21, W22, b22の計6つとなります。
- 層1は単純な線形変換に、活性化関数としてReLU関数を適応したものです。
- 層2は単純な線形変換に、活性化関数として恒等関数を適応したものです。
3.2 Reparameterization Trick
Encoderでμとσを出力してから、zを正規分布からサンプリングします。しかし、ただ単純に正規分布からサンプリングしてしまうと勾配を求めるときに計算が複雑になってしまいます。そこで、Reparametrization Trickという手法を使います。Reparametrization Trickは以下の図の式を使用してzをサンプリングさせる方法です。
$$z = \mu + \epsilon \sigma^2 \hspace{10pt} \epsilon \verb|~| N(0, 1)$$
3.3 Decoderの構造
Decoderの構造は以下の図のようになっています。層は合計で2つありますが、です。DecoderのパラメータはW3, b3, W4, b4の計4つとなります。
- 層3は層1と同じ構造です。
- 層4は単純な線形変換に、活性化関数としてSigmoid関数を適応したものです。

4. 誤差関数
4.1 誤差関数
損失関数は、以下の図のようにErec(再構成誤差)とEreg(正則化項)の和から構成されています。この式の導出については省略します。気になる方は、VAEの変分下界について調べると良いと思います。
$$E = E_{rec} + E_{reg}$$
4.2 再構成誤差
再構成誤差は以下の図の式で定義されています。この式は、入力画像と出力画像が似ているほど値が小さくなる関数です。
$$E_{rec} = \frac{1}{N} \sum_{n}{\sum_{m}{(-x_{nm} \log{y_{nm}} – (1-x_{nm}) \log{(1-y_{nm})})}}$$
4.3 正則化項
正則化項は以下の図の式で定義されています。この式は、zが表順正規分布に近づくほど値が小さくなる関数です。
$$E_{reg} = \frac{1}{N} \sum_{n} \sum_{m} -\frac{1}{2} (1 + \log{\sigma^2_{nm}} – \mu^2_{nm} – \sigma^2_{nm} ) $$
4.4 パラメータの学習について
あとは、上記で定義した誤差関数を最小にするようにパラメータを学習させていけば良いだけです。パラメータの学習については、前の記事を参考してください。



