
損失関数 種類や特徴を解説
記事の目的
ニューラルネットワークで使用する損失関数について解説します。損失関数の概要を初めに解説します。それから、よく使用される損失関数を厳選してその特徴について解説しています。
目次
1. 損失関数の概要
損失関数は、その値が小さければ小さいほどモデルの精度が上がるように設定されます。モデルの学習(パラメータの推定)において、損失関数が減少するようにパラメータを更新するようにします。基本的な損失関数を3つ説明します。
2. 二乗和誤差関数
二乗和誤差関数は回帰問題で恒等関数とセットでよく使用されます。式と勾配とグラフは以下のようになります。
$$E = \frac{1}{2}\sum_{k=1}^{K}{(y_k-t_k)^2}$$
$$\frac{\partial E}{\partial y_k} = y_k-t_k$$
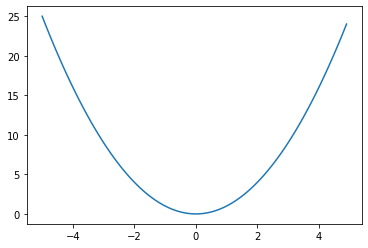
3. バイナリークロスエントロピー誤差関数
バイナリークロスエントロピー誤差は、後述するクロスエントロピー誤差のk=2の場合です。二値の判別問題でSigmoid関数とセットで使用されることが多いです。式と勾配とグラフは以下のようになります。
$$E = -t\log(y)-(1-t)\log(1-y)$$
$$\frac{\partial E}{\partial y} = -\frac{t}{y}+\frac{1-t}{1-y}$$

4. クロスエントロピー誤差
クロスエントロピー誤差は、上記のバイナリークロスエントロピー誤差の多次元に拡張した場合です。多値の判別問題でSoftmax関数とセットで使用されることが多いです。式と勾配とグラフは以下のようになります。
$$E = -\sum_{k=1}^{K}{t_k\log(y_k)}$$
$$\frac{\partial E}{\partial y_k} = -\frac{t_k}{y_k}$$
5. ミニバッチ学習
ミニバッチ学習とは、全データから小さいデータを取り出し全体の近似として計算する方法です。例えば、サンプルサイズが10000のデータに対して100個のデータを無作為に選び出して学習させます。この場合の100個のデータはミニバッチと呼ばれます。
ミニバッチ学習で損失関数を計算する場合は、ミニバッチサイズの平均を出します。例えば、クロスエントロピー誤差をミニバッチ学習で計算した場合は以下のようになります。Nはバッチサイズです。
$$E = -\frac{1}{N}\sum_{n=1}^{N}{\sum_{k=1}^{K}{t_{nk}\log{y_{nk}}}}$$



