
【Rでベイズ統計モデリング#18】時変係数モデル
記事の目的
状態空間モデルである時変係数モデルのベイズ推定を、RとStanを使用して実装していきます。データの作成から実装するので、コピペで再現することが可能です。
目次
0 前準備
0.1 今回のモデル

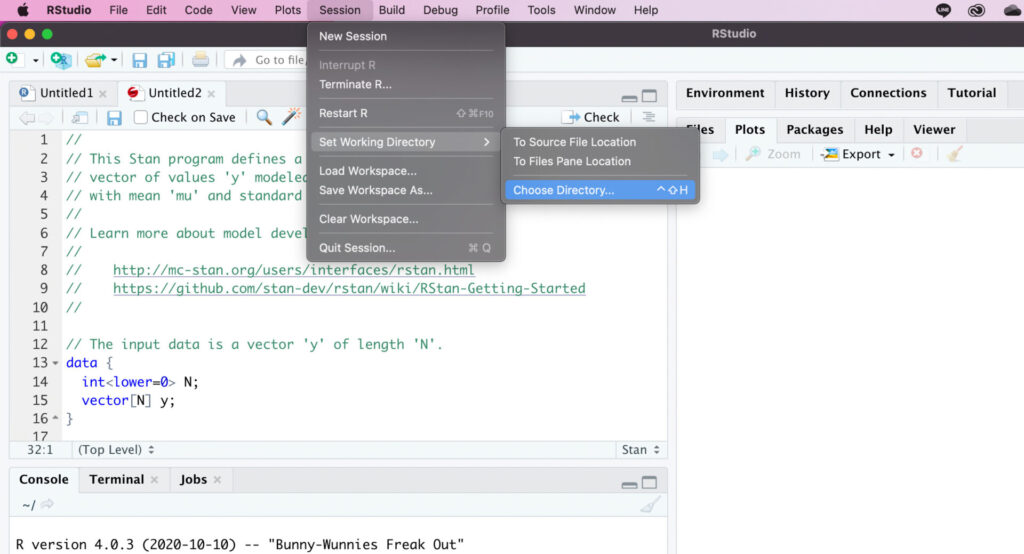
0.2 ワーキングディレクトリの設定
以下の画像のようにワーキングディレクトリを設定します。設定したディレクトリに、RファイルとStanファイルを保存します。
1 ライブラリ
# 1 ライブラリ library(dplyr) library(ggplot2) library(rstan) library(bayesplot) library(gridExtra) set.seed(2) rstan_options(auto_write=TRUE) options(mc.cores=parallel::detectCores())
2 データ
2.1 コード
# 2 データ
## 2.1 データの作成
日付 <- seq(as.POSIXct("2021/05/01"),
as.POSIXct("2021/08/01"), "days")
広告費 <- rnorm(length(日付), 10, 1)
売り上げ<- c()
mu <- c()
b <- c()
mu[1] <- rnorm(1, 80, 5) %>% round(1)
b[1] <- rnorm(1, 10, 1) %>% round(1)
T <- length(日付)
for(t in 2:T){
mu[t] <- rnorm(1, mu[t-1], 5)
b[t] <- rnorm(1, b[t-1], 1)
}
alpha <- mu + b*広告費
for(t in 1:t){
売り上げ[t] <- rnorm(1, alpha[t], 3)
}
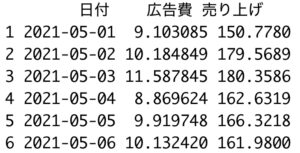
data <- data.frame(日付, 広告費, 売り上げ)
data %>% head()
## 2.2 データの可視化
plot <- data %>%
ggplot(aes(x=日付)) +
theme_classic(base_family = "HiraKakuPro-W3") +
theme(text = element_text(size = 10))+
scale_x_datetime(date_labels = "%m/%d")+
labs(x="日付")
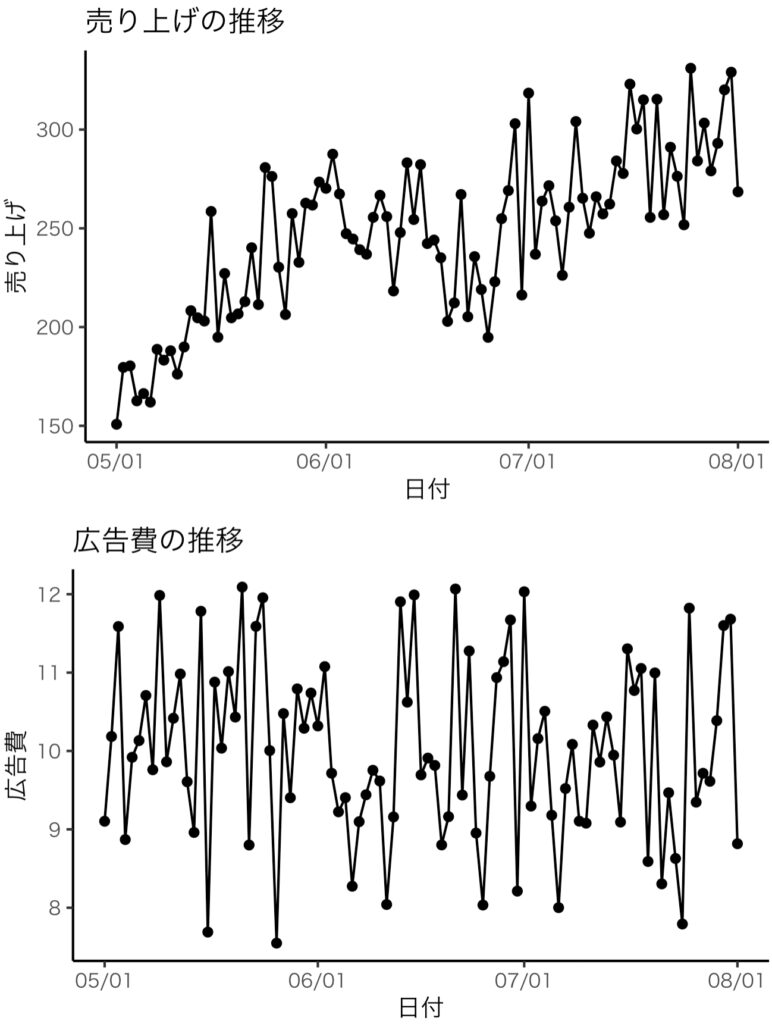
plot1 <- plot +
geom_point(aes(y=売り上げ))+
geom_line(aes(y=売り上げ)) +
labs(y="売り上げ",title="売り上げの推移")
plot2 <- plot +
geom_point(aes(y=広告費))+
geom_line(aes(y=広告費)) +
labs(y="広告費",title="広告費の推移")
grid.arrange(plot1, plot2)
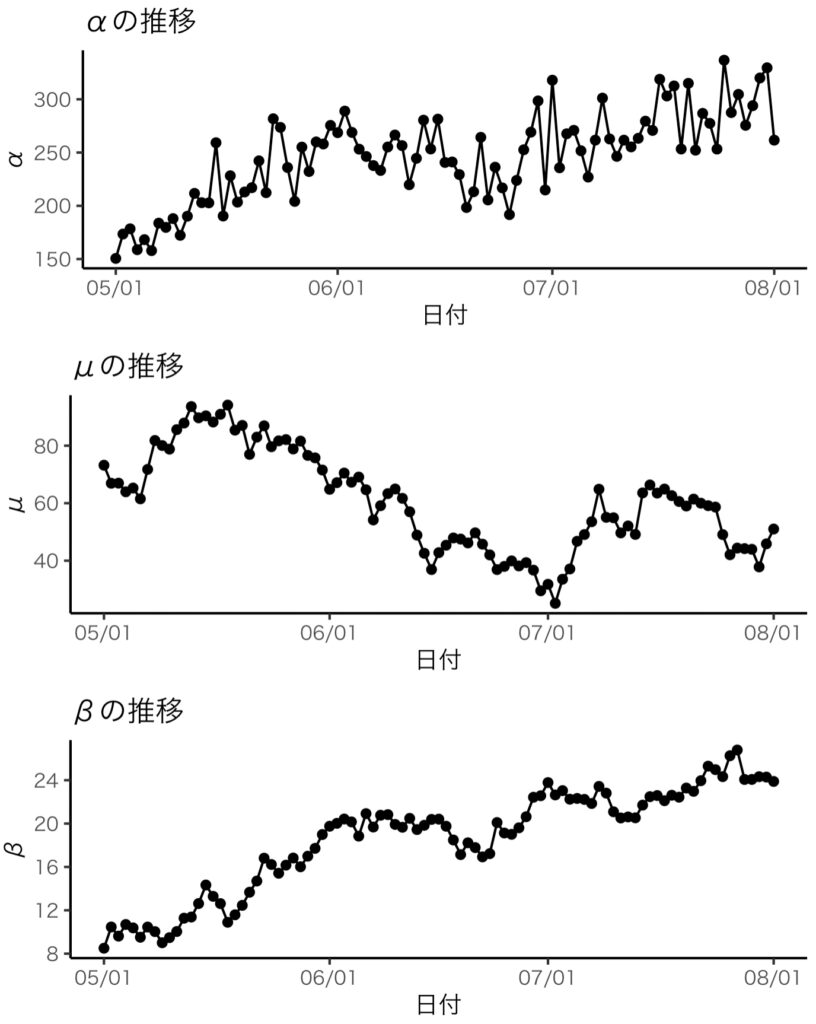
## 2.3 パラメータの可視化
plot_alpha_sim <- plot +
geom_point(aes(y=alpha))+
geom_line(aes(y=alpha)) +
labs(y="α",title="αの推移")
plot_mu_sim <- plot +
geom_point(aes(y=mu))+
geom_line(aes(y=mu)) +
labs(y="μ",title="μの推移")
plot_b_sim <- plot +
geom_point(aes(y=b))+
geom_line(aes(y=b)) +
labs(y="β",title="βの推移")
grid.arrange(plot_alpha_sim, plot_mu_sim, plot_b_sim)
2.2 結果
| 21行目の結果 |
 |
| 41行目の結果 | 59行目の結果 |
 |
 |
3 Stanの利用
3.1 Stanファイル
data {
int T;
vector[T] x;
vector[T] y;
}
parameters {
vector<lower=0>[T] mu;
vector<lower=0>[T] b;
real<lower=0> sigma_w;
real<lower=0> sigma_v;
real<lower=0> sigma_t;
}
transformed parameters{
vector[T] alpha;
for(t in 1:T){
alpha[t] = mu[t] + b[t]*x[t];
}
}
model {
mu[2:T] ~ normal(mu[1:(T-1)], sigma_w);
b[2:T] ~ normal(b[1:(T-1)], sigma_t);
y ~ normal(alpha, sigma_v);
}
generated quantities{
vector[T] y_pred;
for(t in 1:T){
y_pred[t] = normal_rng(alpha[t], sigma_v);
}
}
3.2 Stanを利用するRのコード
# 3 stanの利用 data_list <- list( T = nrow(data), x = data$広告費, y = data$売り上げ ) mcmc_result <- stan( file="18時変係数モデル.stan", data=data_list, seed=1, iter = 2000, warmup = 200, chains = 4, thin=1 )
4 分析結果
4.1 コード
# 4 分析結果
## 4.1 推定結果
print(mcmc_result, pars=c("sigma_w", "sigma_v", "sigma_t"), probs = c(0.025, 0.5, 0.975))
## 4.2 収束の確認
mcmc_sample <- rstan::extract(mcmc_result, permuted=FALSE)
mcmc_combo(mcmc_sample, pars=c("sigma_w","sigma_v", "sigma_t"))
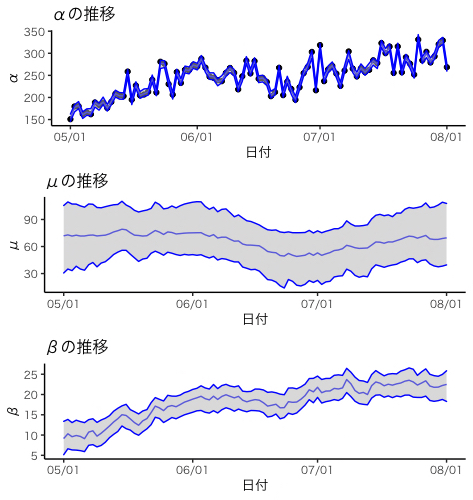
## 4.3 パラメータの確認
mcmc_sample <- rstan::extract(mcmc_result)
func <- function(x){
return (quantile(x, c(0.025, 0.5, 0.975)))
}
alpha <- apply(mcmc_sample[["alpha"]], 2, func)
plot_alpha <- plot +
geom_point(aes(y=売り上げ))+
geom_line(aes(y=alpha[2,]), col="blue") +
geom_ribbon(aes(ymin=alpha[1,],ymax=alpha[3,]), alpha=0.5, fill="gray", col="blue")+
labs(y="α",title="αの推移")
mu <- apply(mcmc_sample[["mu"]], 2, func)
plot_mu <- plot +
geom_line(aes(y=mu[2,]), col="blue") +
geom_ribbon(aes(ymin=mu[1,],ymax=mu[3,]), alpha=0.5, fill="gray", col="blue")+
labs(y="μ",title="μの推移")
b <- apply(mcmc_sample[["b"]], 2, func)
plot_b <- plot +
geom_line(aes(y=b[2,]), col="blue") +
geom_ribbon(aes(ymin=b[1,],ymax=b[3,]), alpha=0.5, fill="gray", col="blue")+
labs(y="β",title="βの推移")
grid.arrange(plot_alpha, plot_mu, plot_b)
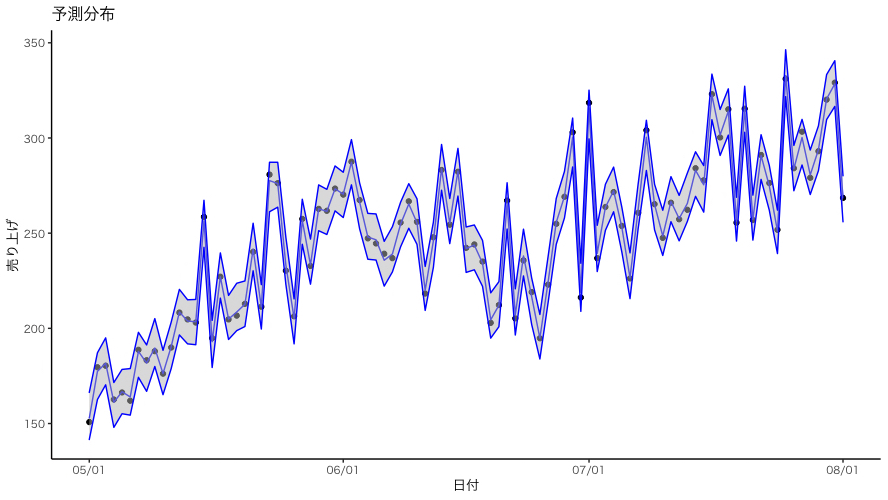
## 4.4 予測分布
y_pred <- apply(mcmc_sample[["y_pred"]], 2, func)
plot +
geom_point(aes(y=売り上げ)) +
geom_line(aes(y=y_pred[2,]), col="blue") +
geom_ribbon(aes(ymin=y_pred[1,],ymax=y_pred[3,]), alpha=0.5, fill="gray", col="blue") +
labs(y="売り上げ",title="予測分布")
4.2 結果
| 3行目の結果 | 7行目の結果 |
 |
 |
| 33行目の結果 | 38行目の結果 |
 |
 |



