
活性化関数 種類や特徴を解説
記事の目的
ニューラルネットワークでよく使用する活性化関数について解説します。活性化関数の概要を初めに解説します。それから、よく使用される活性化関数を厳選して各活性化関数の特徴について解説しています。
目次
1. 活性化関数の概要
1.1 活性化関数とは
活性化関数は、ニューラルネットワークにおいて次の層に値を渡すときに使用される関数です。関数の特徴としては、恒等関数を除けば非線形の関数であることがあげられます。線形の関数を使用すると、いくら層を重ねても結局は線形変換の関数となり意味がなくなってしまうからですあ。
1.2 出力層の活性化関数
出力層に用いられる関数は、大体決められている。回帰の問題を解く場合は二乗和誤差関数がよく使用されます。二値の判別問題であればSigmoid関数、多値の判別問題であればSoftmax関数がよく使用されます。絶対ではないので、注意が必要です。
1.3 勾配の逆伝播
ニューラルネットワークでは誤差逆伝播法で活性化関数の微分を前の層に伝播します。ゆえに、活性化関数選ぶ際には活性化関数の微分(勾配)がどのような値になるのかがとても重要になります。よく問題にあげられるのが勾配の消失です。活性化関数の微分の値が小さくなり、逆伝播すればするほどパラメータが全然更新されなくなってしまったりします。
2. 中間層で使用される関数
2.1 ReLU関数
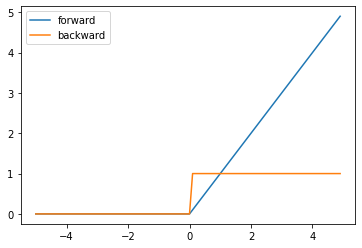
ReLU関数は、以下の図ような関数です。ReLU関数はよく使用されている活性化関数で、特徴としては計算がシンプルで処理が高速です。他にも、後述するSigmoid関数では問題になる勾配の消失が起きないことも特徴的です。
$$h(x) = \begin{cases}x&(x>0)\\0&(x\leq0)\end{cases}$$
$$h'(x) = \begin{cases}1&(x>0)\\0&(x\leq0)\end{cases}$$
2.2 LeakyReLU関数
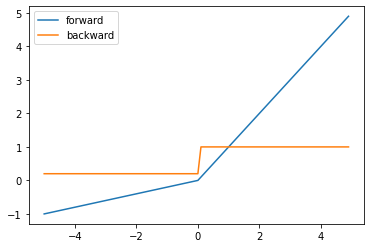
LeakyReLU関数は、以下の図のような関数です。ReLU関数では、出力が0になって学習が進まない場合があります。LeakyReLUでは、入力がマイナスの場合にも少し勾配をつけることでこの問題を回避することができます。
$$h(x) = \begin{cases}x&(x>0)\\ \alpha x&(x\leq0)\end{cases}$$
$$h'(x) = \begin{cases}1&(x>0)\\ \alpha&(x\leq0)\end{cases}$$
3. 出力層で使用される関数
3.1 恒等関数
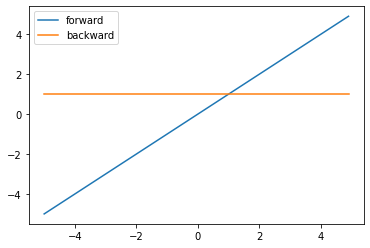
恒等関数は以下の図のような関数です。要するに、何もしない関数です。出力の範囲に制限がないため、回帰問題のときに出力層で使用されることが多いです。
$$h(x) = x$$
$$h'(x) = 1$$
3.2 Sigmoid関数
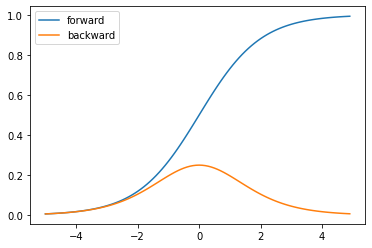
Sigmoid関数は以下の図のような関数です。出力の範囲は0-1で、確率のように扱われています。二値問題のときに出力層で使用されることが多いです。Sigmoid関数のデメリットとして、勾配の消失があります。入力の値が大きかったり、マイナスに大きかったりすると勾配が小さくなり逆伝播でパラメータが更新されなくなってしまう場合があります。
$$h(x) = \frac{1}{1+exp(x)}$$
$$h'(x) = h(x)(1-h(x))$$
3.3 ソフトマックス関数
Softmax関数は以下の図のような関数です。出力結果は多次元のベクトルで、各要素の出力の確率のように扱われています。多値判別問題のときに出力層で使用されることが多いです。
$$h(x_i) = \frac{exp(x_i)}{\sum_{k=1}^{n}{exp(x_k)}}$$
$$h'(x_i) = \sum_{j=1}^{n}{h(x_i)(\delta_{ij} – h(x_i))}$$



