
ニューラルネットワーク 要点解説!【基本】
記事の目的
2層のニューラルネットワークの例を用いて、ニューラルネットワークの理解に必要な知識を解説していきます。具体的には、ニューラルネットワークの構造や、勾配法、誤差逆伝播法などです。なお、今回の例ではMNISTの数字データを使用しています。
目次
1. 使用するデータ
MNISTの数字データを使用します。MNISTの数字データには、以下の図のように数字の画像データとその答えが入っています。
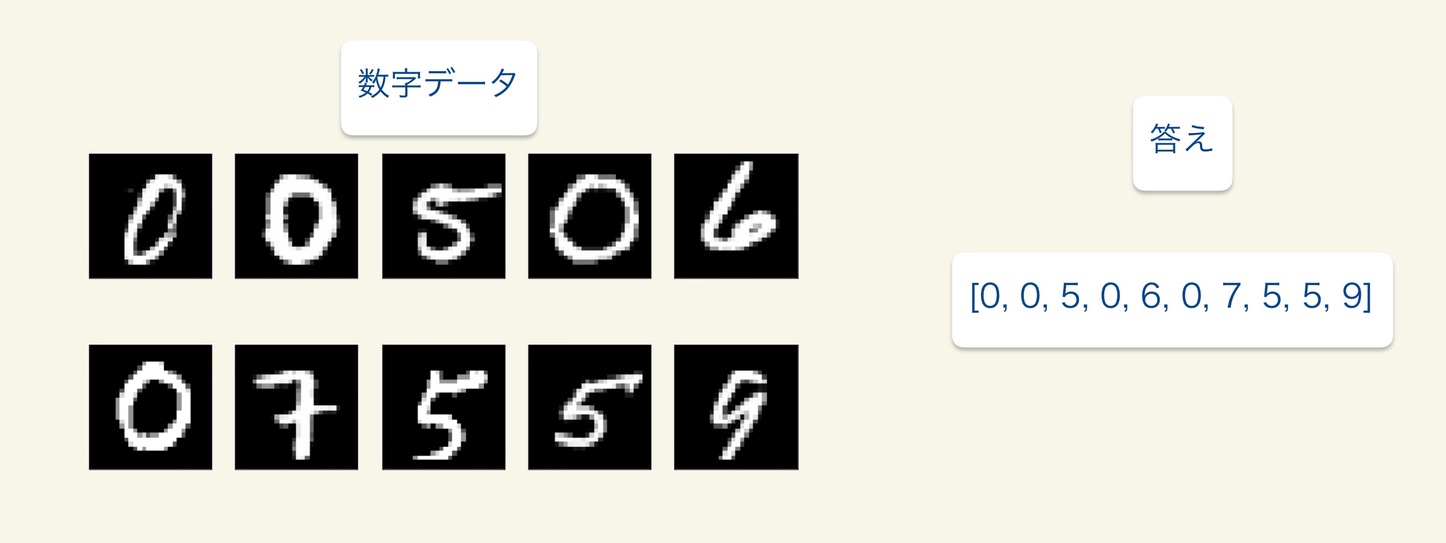
ニューラルネットワークを使用して、未知のMNISTの数字データを判別できるようにします。つまり、0-9のとある数字の画像に対して、その画像の数字が0-9のいくつを表しているのかを判別できるようにするということです。
2. ニューラルネットワークの全体像
2.1 全体像
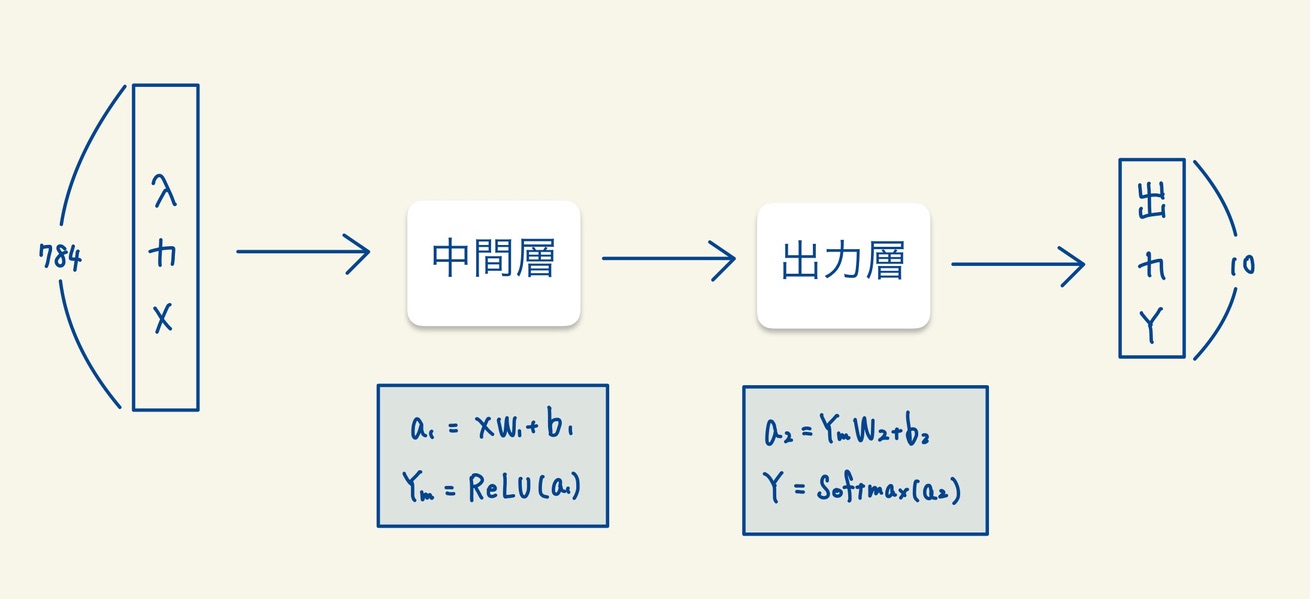
ニューラルネットワークの全体像は以下のようになっています。ニューラルネットワークは簡単に言ってしまえばただの複雑な関数です。今回の例では、入力された画像データ(28×28=784次元のベクトル)に対して10次元(0-9を表す)のベクトルを返す関数です。
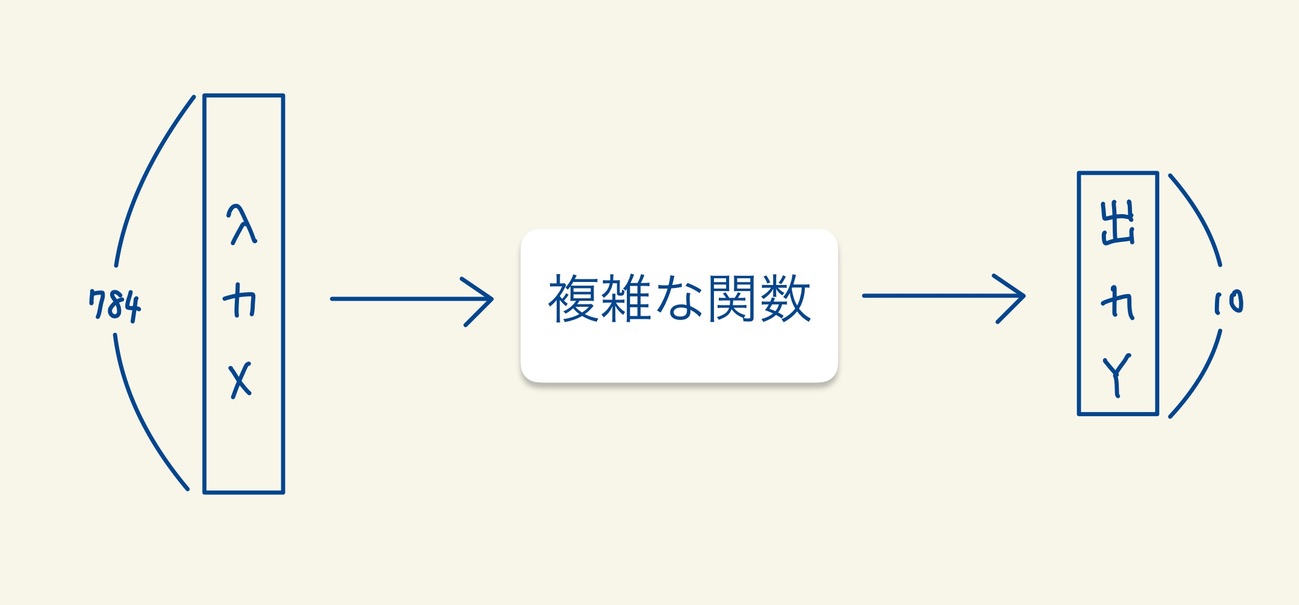
この10次元のベクトルはそれぞれ0-9の数字である確率を表しており、この確率が1番高い数字を判別結果として返します。
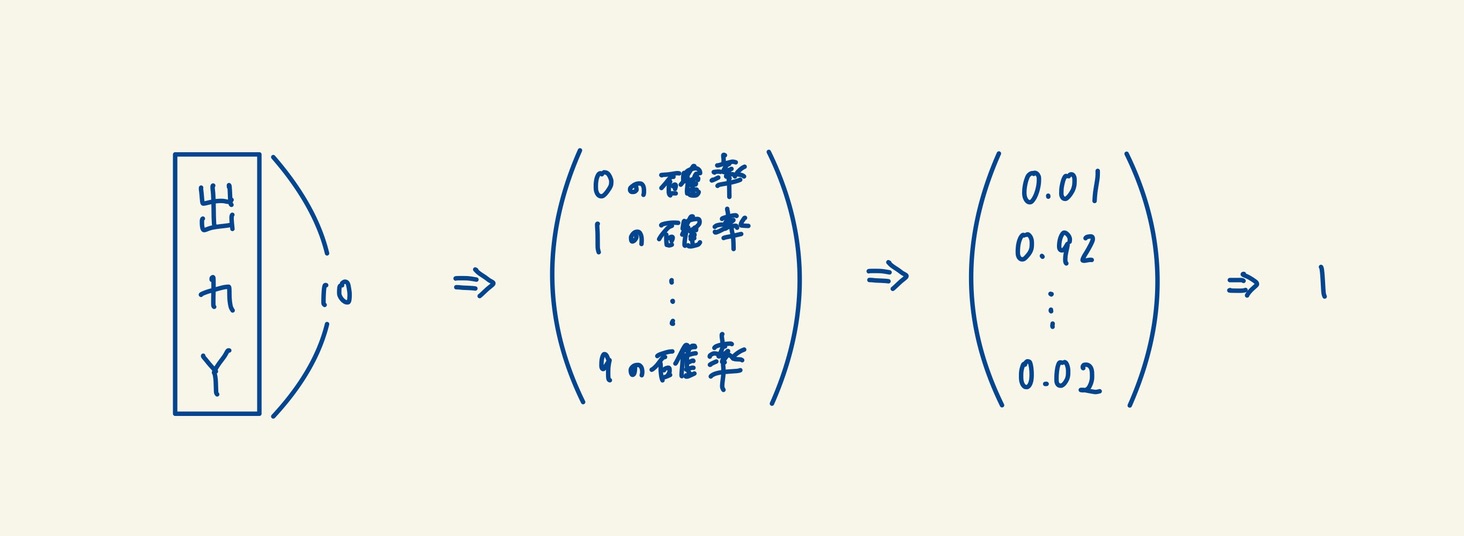
2.2 目的
以上のことから、これから解説することは大きく以下の2つになります。
- 複雑な関数とはどのような関数か
- どのように複雑な関数が判別できるようモデルを学習させるか
3. ニューラルネットワークの構造
3.1 2つの層
それでは、複雑な関数の中身について解説していきます。通常この複雑な関数はいくつもの層が重なってできています。今回の例では、中間層と出力層の2つの層でできています。
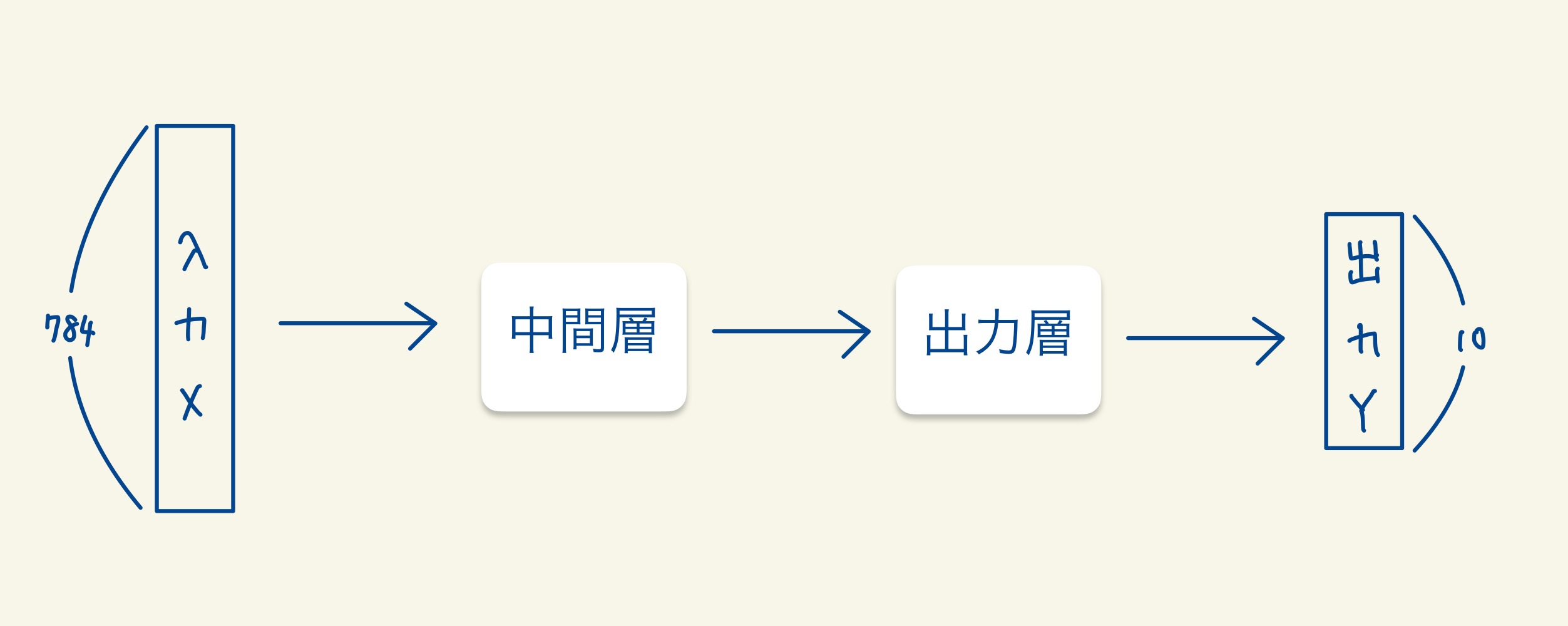
各層の中身は線型結合と活性化関数で構成されています。線型結合によって、入力されたデータの次元を変更させます。そして、非線形の活性化関数を使用して次の層に伝達させます。活性化関数とは、次の層に値を伝播するときに非線形変換を行う役割をもつ関数です。恒等関数といった例外な場合もあります。活性化関数に線形の関数を使用すると、いくら層を重ねても結局は線形変換の関数となり意味がなくなってしまうからです。活性化関数について詳しくはこちら。
3.2 中間層
3.2.1 中間層の線型結合
\(a_1 = X \cdot W_1 + b_1\)
中間層には\(W_1\)と\(b_1\)とパラメータが2つあります。\(W_1\)を784×50の行列とし、\(b_1\)を50次元のベクトルとして、線型結合後の\(a_1\)を50次元となるようにしています。この例では中間層での出力を50次元に設定しています。
3.2.2 中間層の活性化関数
\(Y_m = ReLU(a_1)\)
中間層の活性化関数はReLU関数です。マイナスの入力は0、プラスの入力はそのまま出力する関数です。
3.3 出力層
3.3.1 出力層の線型結合
\(a_2 = Y_m \cdot W_2 + b_2\)
出力層には\(W_2\)と\(b_2\)とパラメータが2つあります。\(W_2\)はを50×10の行列で、\(b_2\)を10次元のベクトルであり線型結合後の\(a_2\)を10次元となるようにします。
3.3.2 出力層の活性化関数
\(Y = Softmax(a_2)\)
出力層の活性化関数はSoftmax関数です。Softmax関数の出力は多次元のベクトルで、各要素の総和が1になるようになっています。この性質により、出力の各要素が確率を表すようになるのです。
4. モデルの学習
4.1 モデルの学習について
上記の説明で、複雑な関数の中身はわかりましたでしょうか。残る説明はモデルの学習(パラメータの最適化)のみです。要は、与えられたデータに対して上記の複雑な関数が正しく出力されるようにパラメータ(\(W_1, b_1, W_2, b_2\))を決めれば良いのです。
4.2 誤差関数
4.2.1 誤差関数の定義
誤差関数には以下の図の交差エントロピー誤差を使用します。yが正解の値の確率を多く割り当てると誤差関数の値は小さくなる関数です。ここで、tは正解のデータです。例えば、入力数字画像の答えが1だった場合\(t = {0, 1, 0, 0, 0, 0, 0, 0, 0, 0}\)です。
$$ E = \ – \sum_{k=1}^{10}{t_k \log{y_k}}$$
4.2.2 誤差関数の例
以下の図が実装の例です。yが正解の値に高い確率を与えられると、誤差関数の値はより小さい値になります。

4.2.3 誤差関数の利用目的
誤差関数の値を小さくする様に、パラメータ(W1,b1,W2,b2)の値を決定すれば良いことになります。このようにパラメータの値を推定していく過程を「モデルの学習」と言います。
4.3 勾配法
4.3.1 勾配法の概要
誤差関数の値を小さくするようにパラメータを更新する方法に、勾配法があります。このパラメータの更新式は以下の図のようになっています。何故このような式になるのかはここでは省きます。この式で実際にうまくいくのかを例を使用して解説していきます。
$$ \theta \leftarrow \theta \ – \ \eta \frac{\partial E}{\partial \theta}$$
4.3.2 勾配法の例
誤差関数として、以下の図の簡単な2次式の例を使用します。まあこの場合θ= 0で、勾配(接線の傾き)が0の場合に誤差関数の値を1番小さくするのは明らかです。ですが、あえて勾配法を使用して解説していきます。
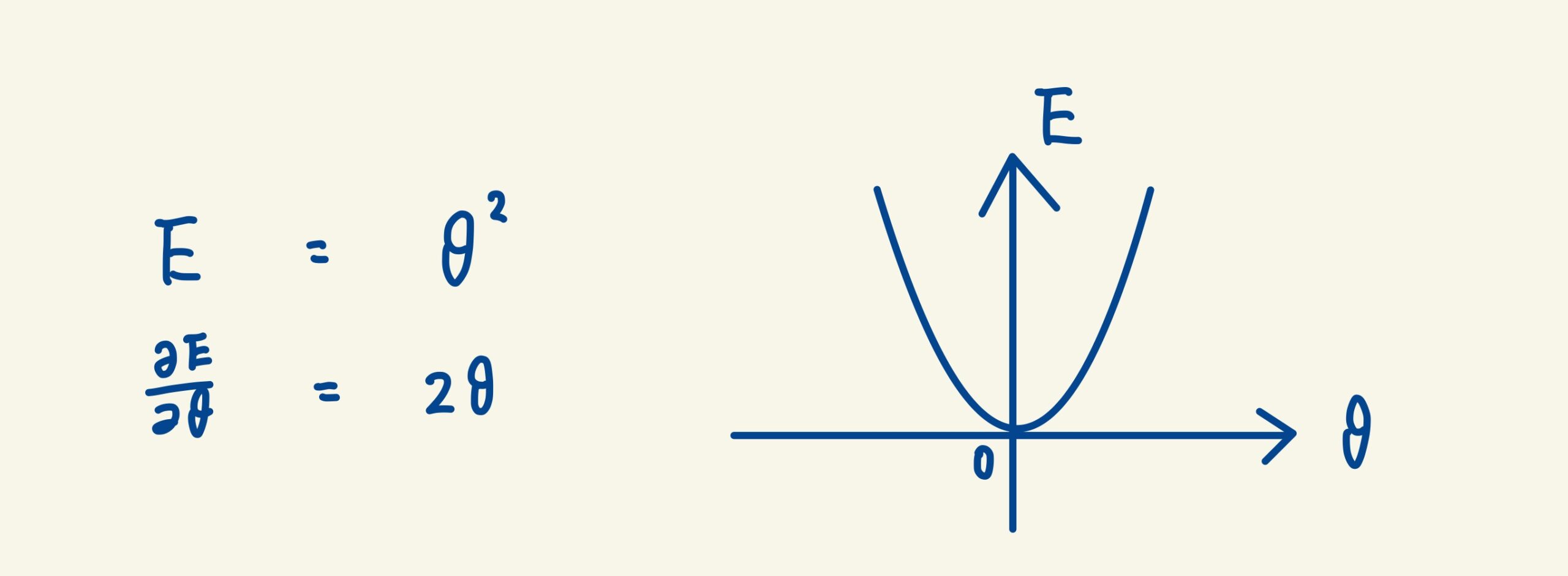
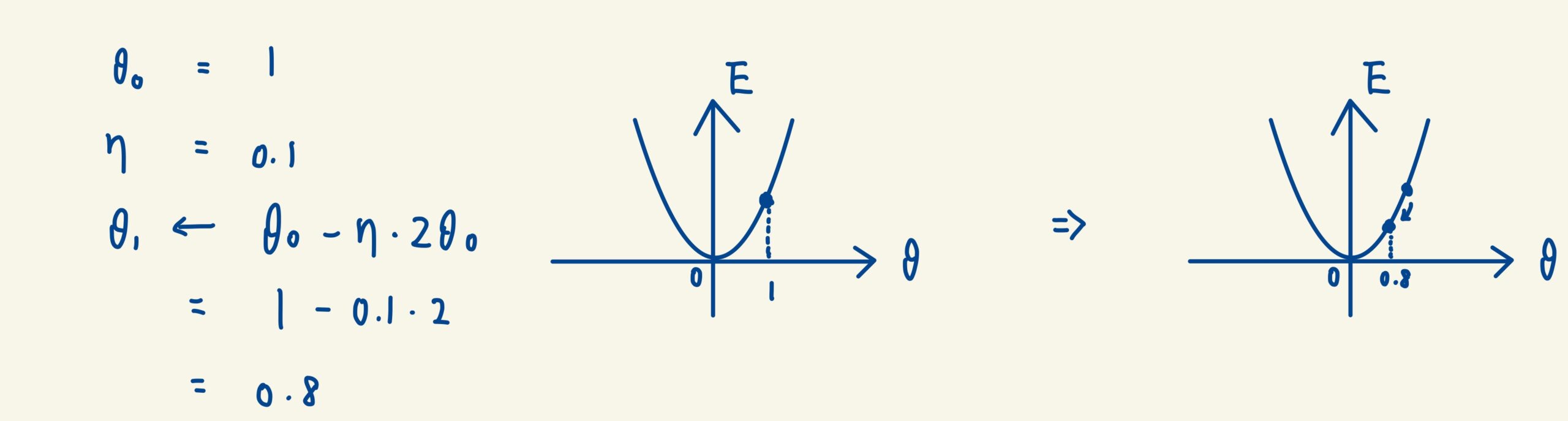
パラメータの初期値を1として、ηを0.1とした例です。ηは学習率といって、パラメータの収束速度を調整する値です。以下の図では、一回の更新でパラメータは1→0.8と、0に近付いていることが確認できます。
今度は、パラメータの初期値を1として、ηを0.01とした例です。この場合もパラメータは-1から-0.98と、0の近づくように更新されています。また、ηの値を小さく設定しているので、更新の幅も小さくなっています。
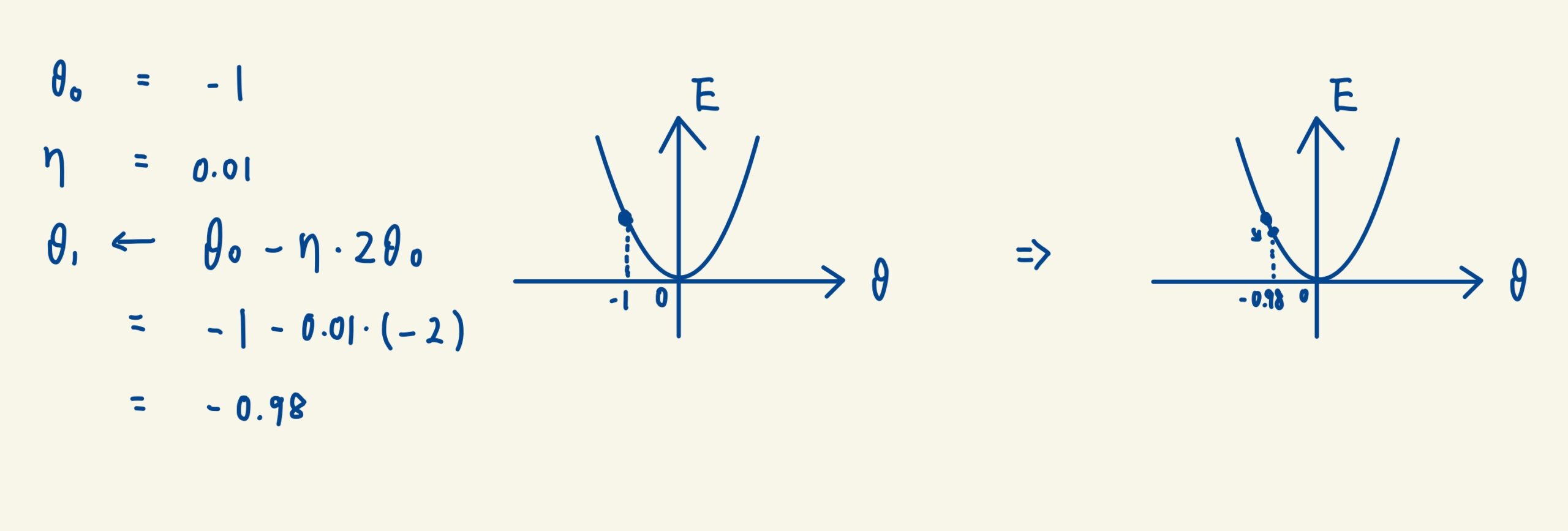
4.4 誤差逆伝播法
4.4.1 誤差逆伝播法の概要
上記の勾配法では、誤差関数をパラメータで微分した値が必要となります。誤差逆伝播とは、一つ後の層の勾配を利用して対象の層の勾配を計算することで、効率的にパラメータの勾配を導出する手法です。
4.4.2 誤差逆伝播法の適応
Step1. 誤差関数の微分
まず初めに、誤差関数をYで微分した値を導出します。これは単純に交差エントロピー誤差の微分です。
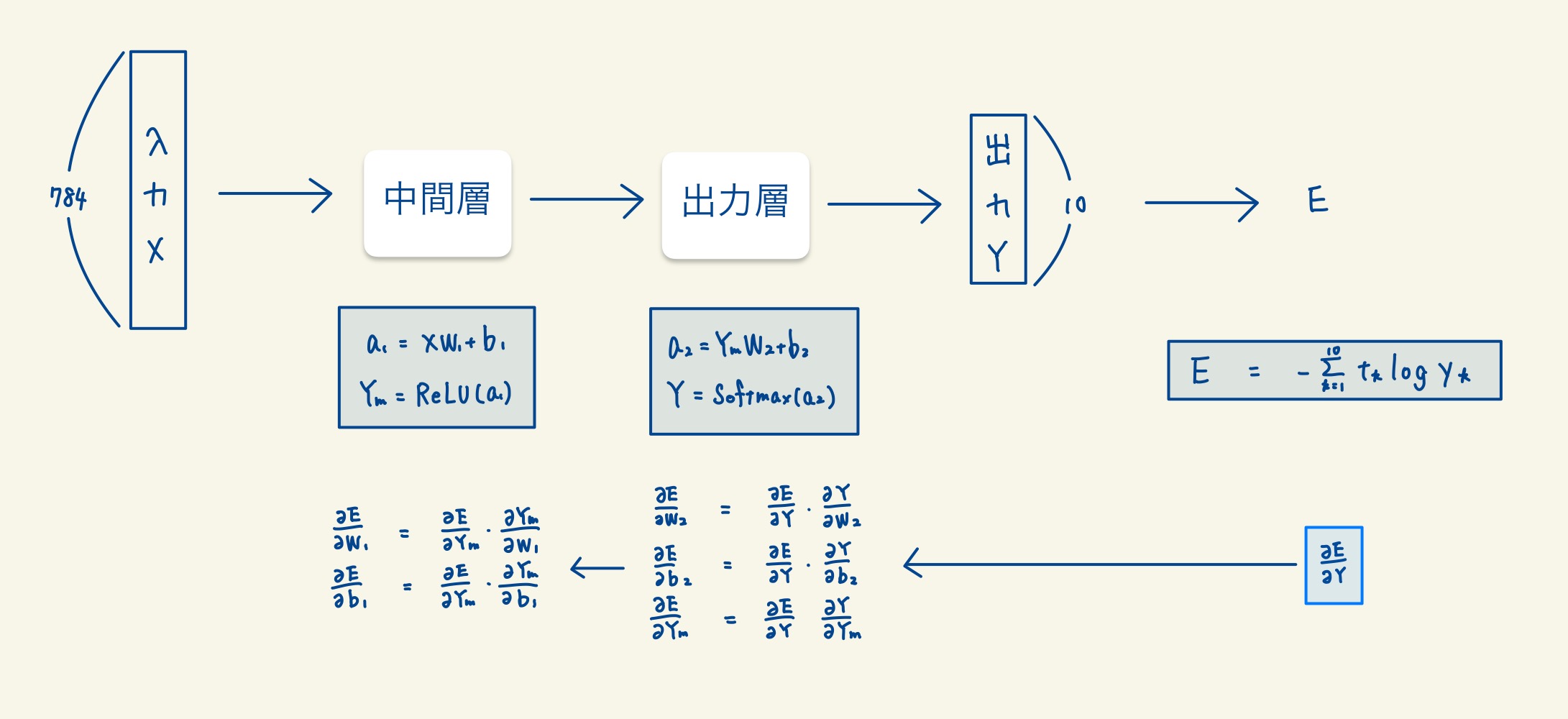
Step2. 出力層の微分
次に、出力層でパラメータでの微分の値と、出力層の入力(Ym)での微分の値を求めます。このとき、Step1で求めた微分の値を使用することで、効率的に求めることができます。
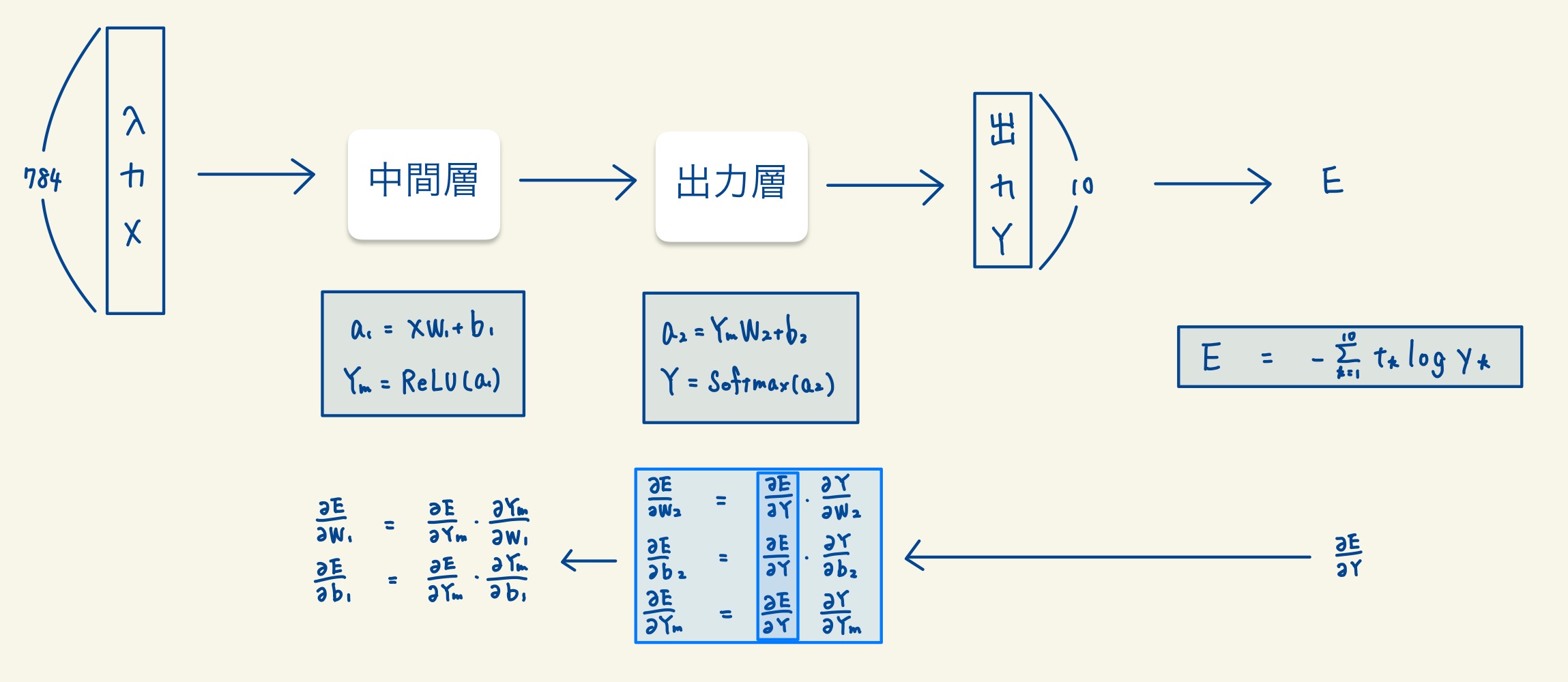
Step3. 中間層の微分
中間層の微分の値は、Step2で求めた値を使用することができます。
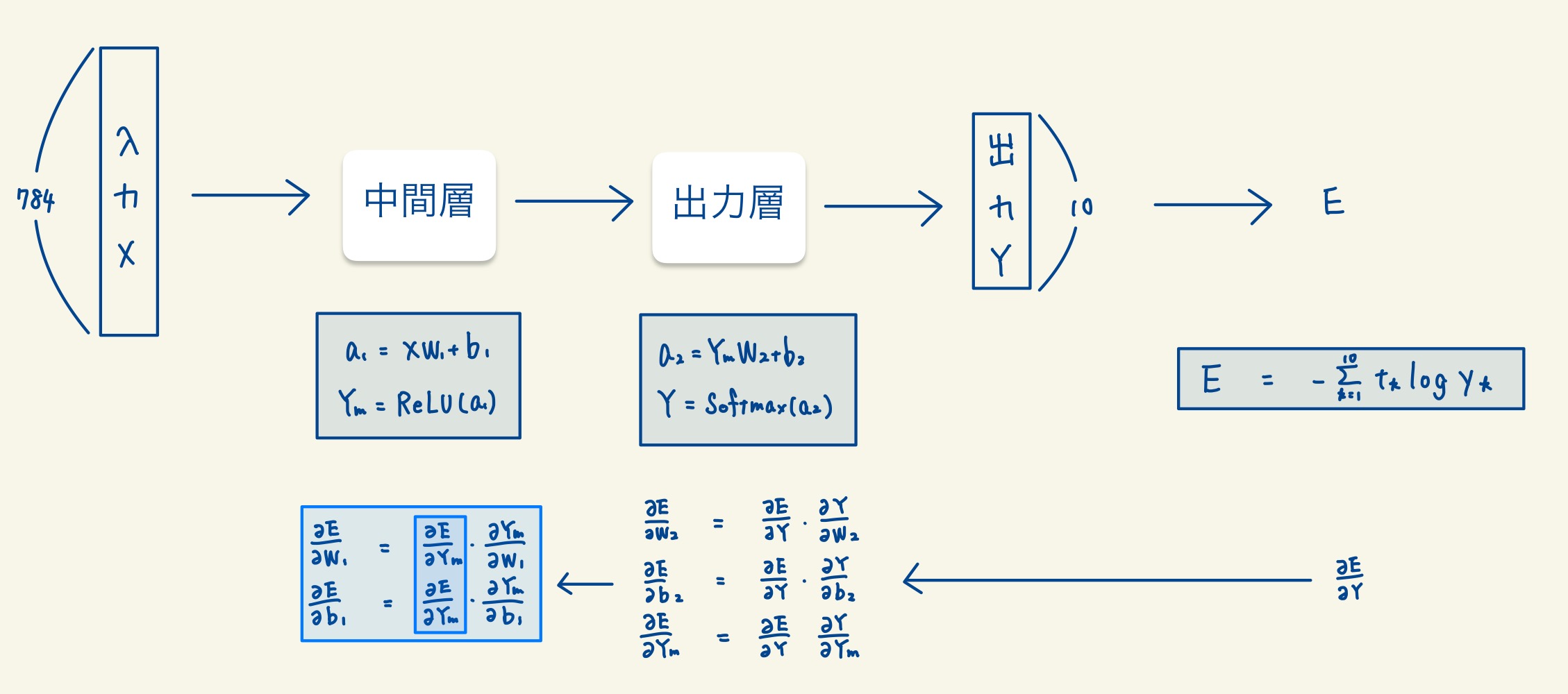
5. まとめ
5.1 全体の流れ
全体の流れを簡単に説明すると以下のようになります。
Step1. 層の構成を決める
Step2. 損失関数を決める
Step3. モデルの学習(以下を繰り返す)
- データを入力して損失関数まで値を求める。
- 誤差逆伝播法でパラメータの微分を求める
- 勾配法でパラメータを更新する
5.2 関連記事
以下に今回と関連する記事を書いているので参考にしてみてください。



