【Rでベイズ統計学#9】多次元ガウス分布(Λ)のベイズ推定

投稿者 Dken2021年11月12日2022年1月28日

記事の目的

多次元ガウス分布(多次元正規分布)のパラメータΛのベイズ推定をRを使用して実装していきます。事前分布にはウィシャート分布を指定して、事後分布を求めていきます。データの作成から実装するので、コピペで再現することが可能です。

目次

ライブラリ
真の分布
事前分布
データ
事後分布

1 ライブラリ

library(ggplot2)
library(ellipse)
library(MCMCpack)
set.seed(1)

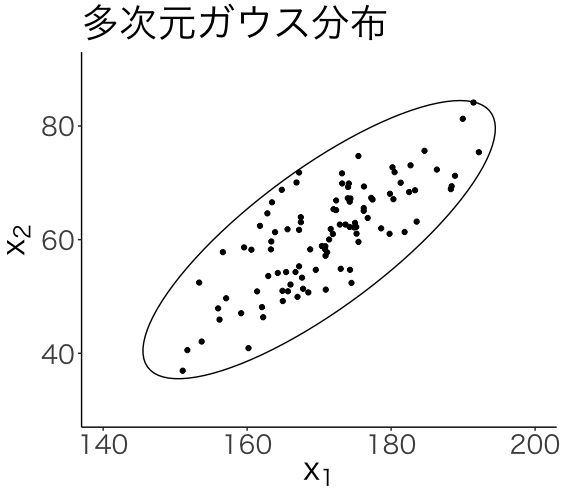
2 真の分布

mu <- c(170, 60)
lambda <- solve(matrix(c(100, 80, 80, 100), ncol = 2))
samples <- mvrnorm(100, mu = mu, Sigma = solve(lambda))

ell <- ellipse(centre=mu, solve(lambda))
ggplot()+
  geom_point(aes(x=samples[,1], y=samples[,2]))+
  labs(x=expression(x[1]), y=expression(x[2]), title="多次元ガウス分布")+
  theme_classic(base_family = "HiraKakuPro-W3") +
  theme(text = element_text(size = 24))+
  lims(x=c(140,200), y=c(30,90))+
  geom_polygon(data=as.data.frame(ell), aes(x,y), fill=NA,colour="black")

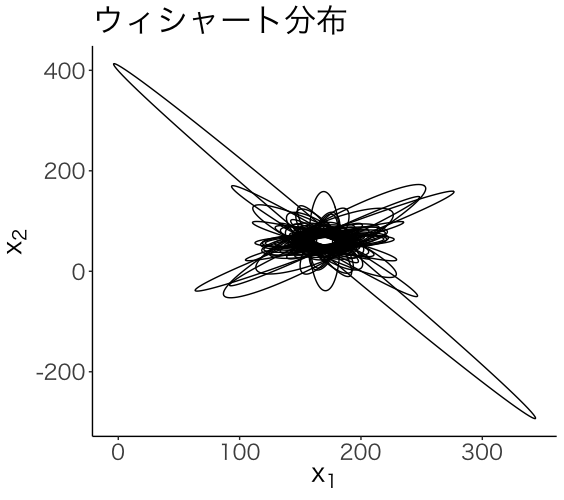
3 事前分布

n_pre <- 3
w_pre <- diag(2)*0.01
lambda_sample_pre <- rwish(n_pre, w_pre)

plot <- ggplot() +
  theme_classic(base_family = "HiraKakuPro-W3")+
  theme(text = element_text(size = 20), legend.position=c(0.3,0.7)) +
  labs(x=expression(x[1]), y=expression(x[2]), title="ウィシャート分布") 
for(i in 1:100){
  lambda_samples_pre <- rwish(n_pre, w_pre)
  ell <-  ellipse(centre=mu, solve(lambda_samples_pre))
  plot <- plot + geom_polygon(data=as.data.frame(ell),aes(x,y), fill=NA,colour="black")
}
plot

4 データ

data <- mvrnorm(100, mu = mu, Sigma = solve(lambda))
N <- nrow(data)

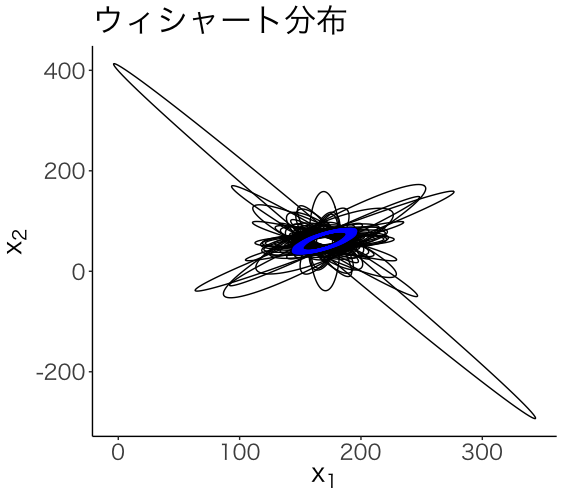
5 事後分布

n_pos <- N + n_pre
S <- 0
for(i in 1:N){
  S <- S + (data[i,]-mu) %*% t(data[i,]-mu)
}
w_pos <- solve(S + solve(w_pre))

for(i in 1:100){
  lambda_samples_pos <- rwish(n_pos, w_pos)
  ell <-  ellipse(centre=mu, solve(lambda_samples_pos))
  plot <- plot + geom_polygon(data=as.data.frame(ell),aes(x,y), fill=NA, colour="blue")
}
plot