
【Rでベイズ統計モデリング#8】ロジスティック回帰モデル(brms)
記事の目的
GLMである正規線形モデルのベイズ推定を、RとStanを使用して実装していきます。今回は、「brms」というライブラリを使用します。データの作成から実装するので、コピペで再現することが可能です。
目次
0 前準備
0.1 今回のモデル

0.2 ワーキングディレクトリの設定
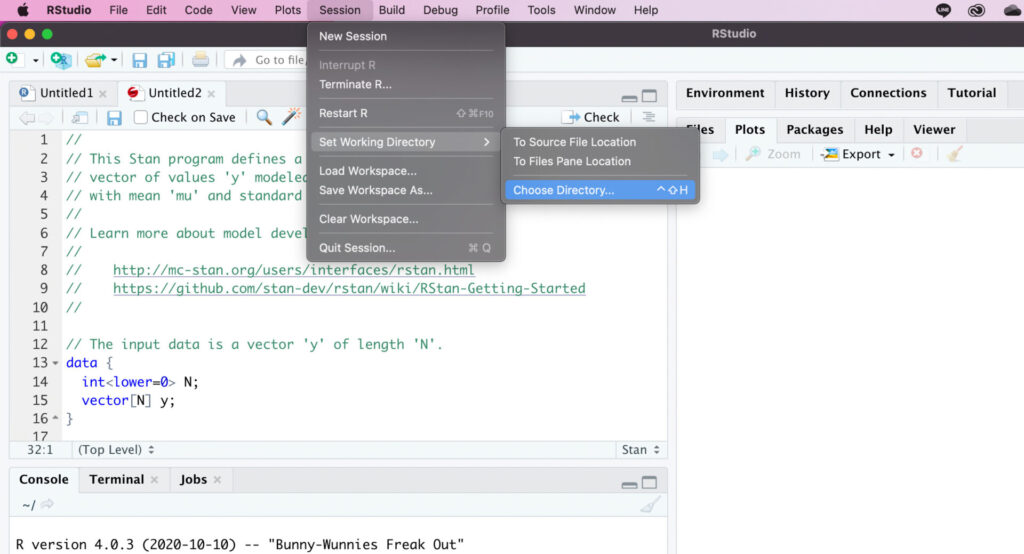
以下の画像のようにワーキングディレクトリを設定します。設定したディレクトリに、RファイルとStanファイルを保存します。
1 ライブラリ
# 1 ライブラリ library(dplyr) library(ggplot2) library(rstan) library(brms) library(patchwork) set.seed(1) rstan_options(auto_write=TRUE) options(mc.cores=parallel::detectCores())
2 データ
2.1 コード
# 2 データ
資格 <- rbinom(100, 1, 0.3)
年齢 <- rnorm(100, 50, 20) %>% round()
p <- 1/(1+exp(-(10-0.4*年齢 + 7*資格)))
試験 <- rbinom(100, 1, p)
data <- data.frame(資格, 年齢, 試験) %>% filter(年齢>18, 年齢<65)
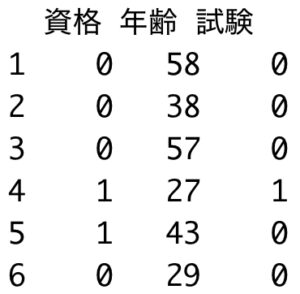
data %>% head()
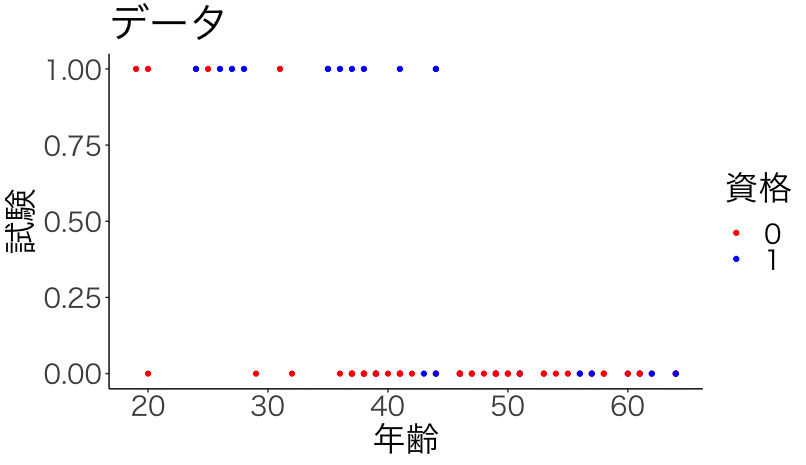
plot <- ggplot() +
geom_point(aes(x=data$年齢, y=data$試験, color=factor(data$資格))) +
theme_classic(base_family = "HiraKakuPro-W3") +
theme(text=element_text(size=25))+
labs(x="年齢", y="試験", title="モデル") +
scale_color_manual("資格",values=c("red","blue"))
plot
2.2 結果
| 7行目の結果 | 15行目の結果 |
 |
 |
3 brmsの利用
# 3 brmsの使用 mcmc_result <- brm( data = data, formula = 試験~ 年齢 + 資格, family = bernoulli(), seed = 1, iter = 1000, warmup = 200, chains = 4, thin=1 )
4 分析結果
4.1 コード
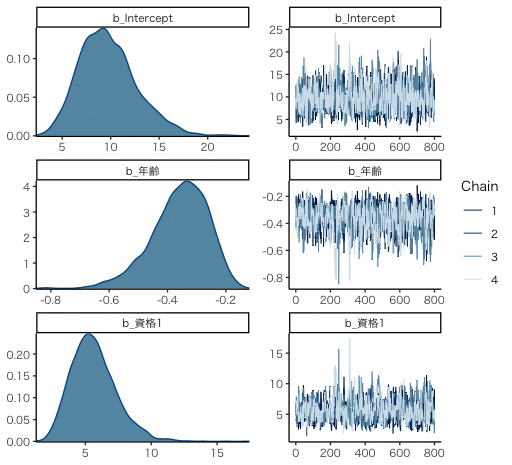
# 4 分析結果 ## 4.1 推定結果 print(mcmc_result) ## 4.2 収束の確認 theme_set(theme_classic(base_size = 10, base_family = "HiraKakuProN-W3")) plot(mcmc_result) ## 4.3 pの確認 plot(conditional_effects(mcmc_result, effects="年齢:資格"), points=TRUE) %>% wrap_plots() + plot_annotation(title="pの推定結果") ## 4.4 予測分布 plot(conditional_effects(mcmc_result, effects="年齢:資格", method="predict"), points=TRUE)%>% wrap_plots() + plot_annotation(title="予測分布")
4.2 結果
| 3行目の結果 | 7行目の結果 |
 |
 |
| 10行目の結果 | 14行目の結果 |
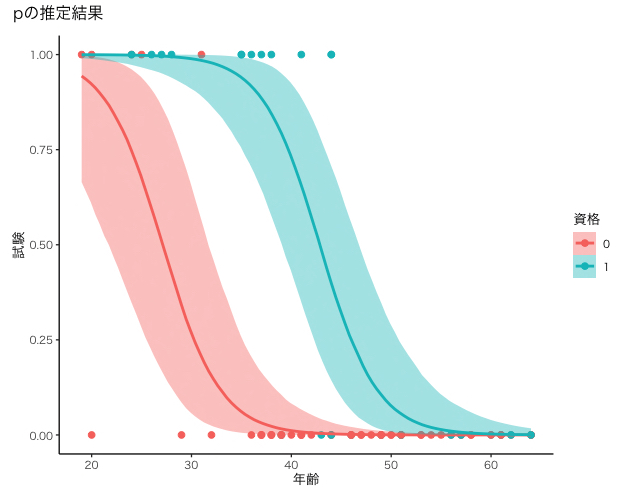 |
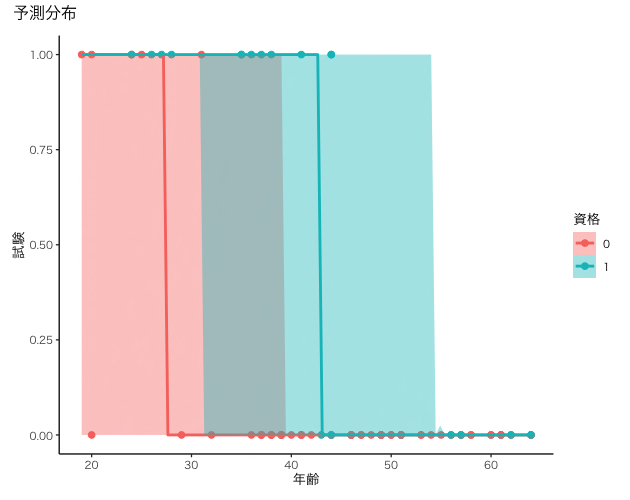 |



