【Rで統計学#1】1次元データの記述統計 - データサイエンス研究所

記事の目的

R言語を使用して、1次元データの記述統計について実装していきます。
この内容を解説しているYoutube動画があるので是非みてみてください！

1 使用するライブラリとデータの作成

1.1 使用するライブラリ

install.packages("dplyr") # 一度もインストールしていない場合
install.packages("ggplot2") # 一度もインストールしていない場合
install.packages("psych") # 一度もインストールしていない場合
library(dplyr)
library(ggplot2)
library(psych)

1.2 データの作成

set.seed(10)
性別 <- sample(c("男性", "女性"), size=100, replace = TRUE) # 男性、女性のサンプルを100個
成績 <- sample(c("A", "B", "C"), size=100, replace = TRUE) # A, B, Cのサンプルを100個
偏差値 <- rnorm(100, 50, 10) %>% round(1) # 偏差値~N(50,10)
身長 <- rnorm(100, 170, 10) %>% round() # 偏差値~N(50,10)
data <- data.frame(性別, 成績, 偏差値, 身長)
head(data) # データ確認

2 棒グラフ(質的データの可視化)

2.1 棒グラフ1 (性別のプロット)

data %>%
  ggplot(aes(性別)) + # 軸の設定
  geom_bar() + # 棒グラフ
  theme_classic(base_family = "HiraKakuPro-W3") + # テーマと文字化け修正
  theme(text=element_text(size=30)) + # 文字サイズ
  labs(title="棒グラフ") # タイトル

2.2 棒グラフ2(成績のプロット)

data %>%
  ggplot(aes(成績)) + # 軸の指定
  geom_bar() + # 棒グラフ
  theme_classic(base_family = "HiraKakuPro-W3") + # テーマと文字化け修正
  theme(text=element_text(size=30)) + # 文字サイズ
  labs(title="棒グラフ") # タイトル

3 ヒストグラム(量的データの可視化)

3.1 ヒストグラム1(身長の可視化)

data %>%
  ggplot(aes(身長))+ # 軸の設定
  geom_histogram(binwidth = 10, col="white") + # ヒストグラムと幅(binwidth)と色(col)
  theme_classic(base_family = "HiraKakuPro-W3") + # テーマと文字化け修正
  theme(text=element_text(size=30)) + # 文字サイズ
  labs(title="ヒストグラム") # タイトル

3.2 ヒストグラム2(偏差値の可視化)

data %>%
  ggplot(aes(偏差値))+ # 軸の設定
  geom_histogram(breaks=seq(0,100,10), col="white") + # ヒストグラムと幅(breaks)と色(col)
  theme_classic(base_family = "HiraKakuPro-W3") + # テーマと文字化け修正
  theme(text=element_text(size=30)) + # 文字サイズ
  labs(title="ヒストグラム") # タイトル

4 1次元データの代表値

4.1 1次元データの代表値

平均値 <- mean(data$身長)
中央値 <- median(data$身長)
最頻値 <- data$身長 %>% table() %>% which.max() %>% names()
四分位点 <- quantile(data$身長)
パーセンタイル <- quantile(data$身長, c(0.05,0.95))
平均値 ; 中央値 ; 最頻値 ; 四分位点 ; パーセンタイル

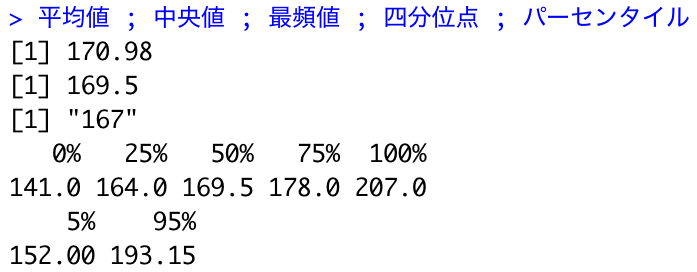
4.2 平均値

$$\bar x = \frac{1}{N} \sum_n x_n$$

平均値2 <- sum(data$身長)/nrow(data) # 平均値の計算
平均値 ; 平均値2

5 1次元データのばらつき

5.1 1次元データのばらつき

不偏分散 <- var(data$身長)
標準偏差 <- sd(data$身長)
レンジ <- max(data$身長) - min(data$身長)
四分位範囲 <- (quantile(data$身長)[4]- quantile(data$身長)[2])/2
不偏分散 ; 標準偏差 ; レンジ ; 四分位範囲[[1]]

5.2 不偏分散

$$U = \frac{1}{N-1} \sum_n (x_n – \bar x)^2 $$

不偏分散2 <- sum((data$身長-mean(data$身長))^2)/(nrow(data)-1) # 不偏分散の計算
不偏分散 ; 不偏分散2

5.3 分散

$$ s^2 = \frac{1}{N} (x_n-\bar x)^2 $$

$$ s^2 = \bar{x^2} – {\bar x}^2 $$

分散 <- sum((data$身長-mean(data$身長))^2)/nrow(data) # 分散の計算
分散2 <- mean(data$身長^2) - mean(data$身長)^2 # 分散の公式
分散 ; 分散2

6 Rの便利な関数

6.1 summary関数

summary(data)

6.2 describe関数

describe(data)

7 apply関数

7.1 各列の平均

data[,3:4] %>% apply(2,mean) # 各列の平均値

7.2 各列の標準偏差

data[,3:4] %>% apply(2,mean) # 各列の平均値