【Rで統計学#6】区間推定

投稿者 Dken2021年8月14日2021年9月16日

記事の目的

R言語を使用して、区間推定について実装していきます。

目次

使用するライブラリとデータの作成
区間推定μ(σ既知)
区間推定μ
区間推定σ

1 使用するライブラリとデータの作成

1.1 使用するライブラリ

install.packages("dplyr") # 一度もインストールしていない場合
install.packages("ggplot2") # 一度もインストールしていない場合
library(dplyr)
library(ggplot2)

1.2 データの作成

set.seed(100)
身長 <- rnorm(100, 170, 10) %>% round()
x <- 身長
N <- length(x)

2 区間推定μ(σ既知)

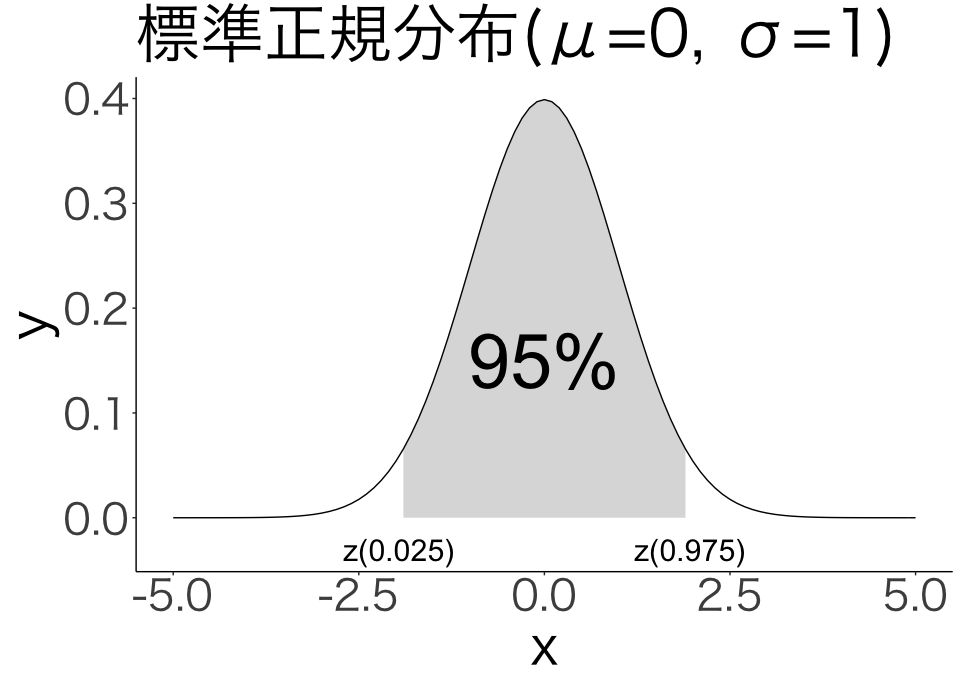
2.1 標準正規分布

x1 <- seq(-5,5,0.1)
y1 <- dnorm(x1, 0, 1)
ggplot() +
  geom_line(aes(x1, y1)) +
  theme_classic(base_family="HiraKakuPro-W3") +
  theme(text=element_text(size=40)) +
  labs(x="x", y="y", title="標準正規分布(μ=0, σ=1)") +
  geom_ribbon(aes(x1[qnorm(0.025)<=x1&x1<=qnorm(0.975)],y1[qnorm(0.025)<=x1&x1<=qnorm(0.975)],ymin=0,ymax=y1[qnorm(0.025)<=x1&x1<=qnorm(0.975)]), alpha=0.2) +
  annotate("text", x=0, y=0.15, label="95%", size=20) +
  annotate("text", x=qnorm(0.975), y=-0.03, label="z(0.975)", size=8) +
  annotate("text", x=qnorm(0.025), y=-0.03, label="z(0.025)", size=8)

2.2 区間推定μ(σ既知)

xbar <- mean(x)
z <- qnorm(0.975, 0, 1)
xbar - z*sqrt(10^2/N) ; xbar + z*sqrt(10^2/N)

3 区間推定σ

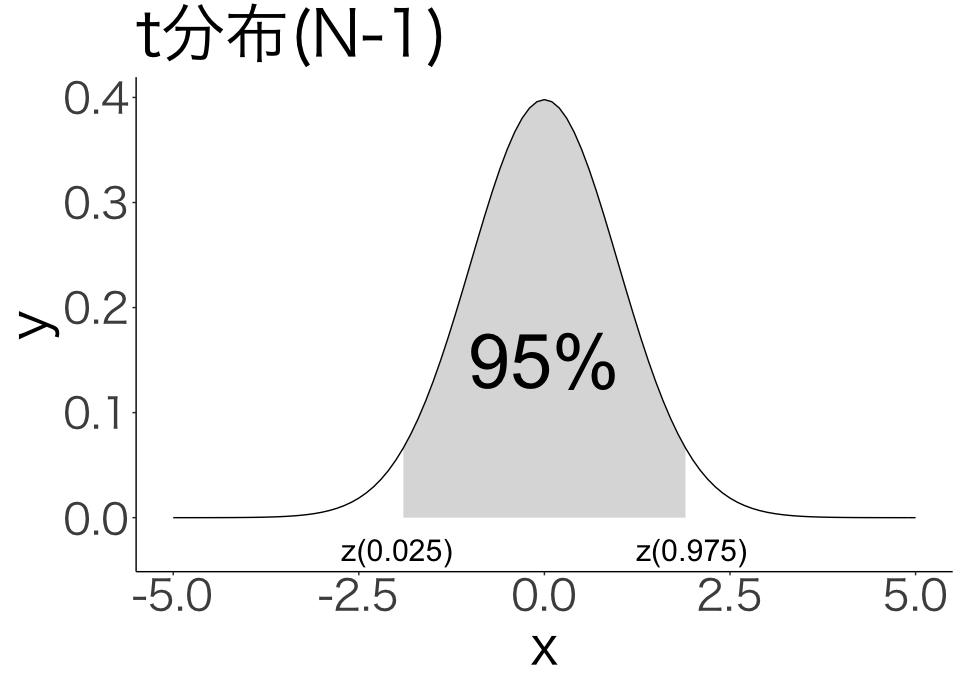
3.1 t分布

x2 <- seq(-5,5,0.1)
y2 <- dt(x2,N-1)
ggplot() +
  geom_line(aes(x2, y2)) +
  theme_classic(base_family="HiraKakuPro-W3") +
  theme(text=element_text(size=40)) +
  labs(x="x", y="y", title="t分布(N-1)") +
  geom_ribbon(aes(x2[qt(0.025, N-1)<=x2&x2<=qt(0.975, N-1)],y2[qt(0.025, N-1)<=x2&x2<=qt(0.975, N-1)],ymin=0,ymax=y2[qt(0.025, N-1)<=x2&x2<=qt(0.975, N-1)]), alpha=0.2) +
  annotate("text", x=0, y=0.15, label="95%", size=20) +
  annotate("text", x=qt(0.975, N-1), y=-0.03, label="z(0.975)", size=8) +
  annotate("text", x=qt(0.025, N-1), y=-0.03, label="z(0.025)", size=8)

3.2 区間推定μ

xbar <- mean(x)
S2 <- sum((x-xbar)^2)/N
u <- qt(0.975, N-1)
xbar - u*sqrt(S2/(N-1)) ; xbar + u*sqrt(S2/(N-1))

4 区間推定σ

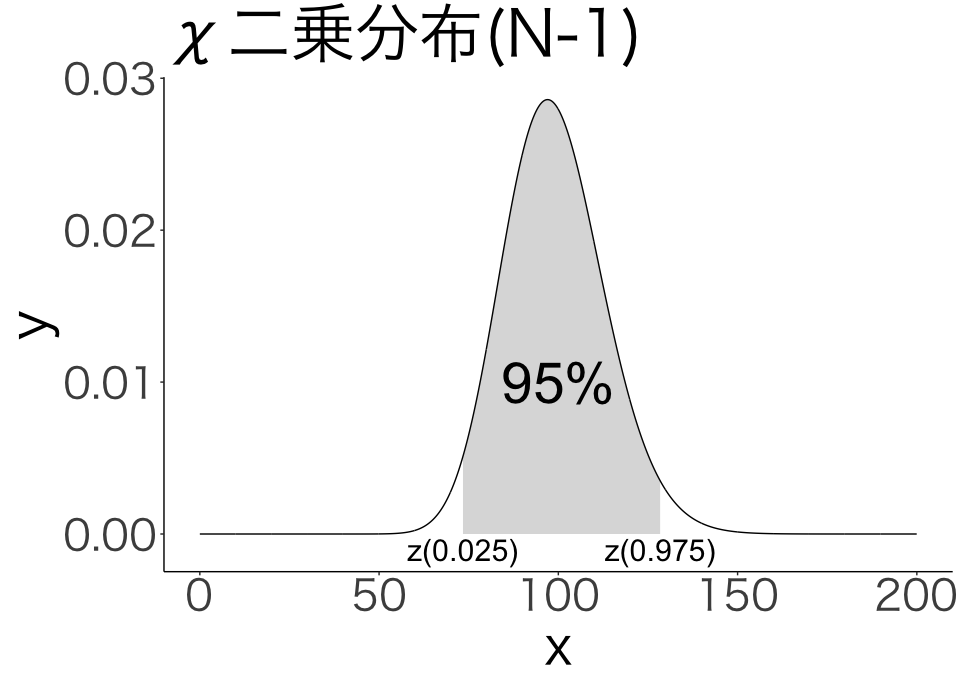
4.1 χ二乗分布

x3 <- seq(0,200,0.1)
y3 <- dchisq(x3,N-1)
ggplot() +
  geom_line(aes(x3, y3)) +
  theme_classic(base_family="HiraKakuPro-W3") +
  theme(text=element_text(size=40)) +
  labs(x="x", y="y", title="χ二乗分布(N-1)") +
  geom_ribbon(aes(x3[qchisq(0.025, N-1)<=x3&x3<=qchisq(0.975, N-1)],y3[qchisq(0.025, N-1)<=x3&x3<=qchisq(0.975, N-1)],ymin=0,ymax=y3[qchisq(0.025, N-1)<=x3&x3<=qchisq(0.975, N-1)]), alpha=0.2) +
  annotate("text", x=N, y=0.01, label="95%", size=15) +
  annotate("text", x=qchisq(0.975, N-1), y=-0.001, label="z(0.975)", size=8) +
  annotate("text", x=qchisq(0.025, N-1), y=-0.001, label="z(0.025)", size=8)

4.2 区間推定σ

v1 <- qchisq(0.025, N-1)
v2 <- qchisq(0.975, N-1)
N*S2/v2 ; N*S2/v1